交换图表
在数学领域,尤其是范畴论中,通常使用以对象为顶点、态射为边的交换图表来直观的表达一些性质,尤其是泛性质。
在图表中,复合连接任意两个对象的不同路径上的态射,所得的结果均相等,则称此图表可交换。同时,按照惯例,实线通常表示任意给定的态射,虚线则表示存在或唯一存在的态射。
举例
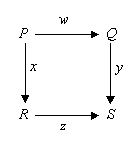
- 下面的正方形为可交换,如果满足条件:y o w = z o x。
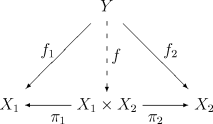
- 如下表明积的泛性质的图表可交换。此图表意味着,对任意存在态射f1 : Y → X1和f2 : Y → X2的对象Y,在同構的意義下,存在唯一态射f,满足:
- π1 o f = f1
- π2 o f = f2
|
|---|
| |
高階範疇論 |
|---|
| 基本概念 | |
|---|
| n-範疇 | | 弱 n-範疇 |
- 雙範疇
- 三範疇
- 四範疇
- 闞複形
- ∞-廣群
- ∞-拓撲斯
|
|---|
| 強 n-範疇 | |
|---|
|
|---|
| 範疇化概念 |
- 2-群
- 2-環
- En-環
- (對稱) 么半範疇
- n-群
- n-么半群
|
|---|
|
|
|